Am 1. Juni 1631 heiratete Fermat Louise de Long, eine Cousine
mütterlicherseits.
Am 20. August 1601 wurde Pierre de Fermat in Beaumont de Lomagne
als Sohn eines Lederhändlers geboren.
Er studierte in Toulouse Rechtswissenschaften, wurde Anwalt und bekleidete ab 1631 verschiedene Ämter am obersten Gerichtshof zu Toulouse. Über seine Studienzeit ist nur bekannt, daß er sehr gute Kenntnisse aller führenden europäischen Sprachen der damaligen Zeit sowie Griechisch und Latein hatte. Er verfaßte etliche Gedichte in spanischer und französischer Sprache.
Die Mathematik betrieb er nur als Hobby, wobei sein Interesse zunächst nur der antiken Mathematik galt, wie Schriften von Euklid und Apollonios. 1628 / 29 entwickelte Fermat eine Methode der Maxima und Minima. Bei dieser Methode handelte es sich um eine verkappte Differentialrechnung, welche den Methoden von Leibniz und Newton sehr nahe steht. Durch seine Berufstätigkeit als Anwalt wurde er am 1. Mai 1631 in den Adelsstand erhoben.
Am 1. Juni 1631 heiratete Fermat Louise de Long, eine Cousine
mütterlicherseits.
Nach der Lektüre einiger Werke von François Vieta enstand um 1635, also vor dem Erscheinens von Rene Descartes "Discours de la méthode", Fermats Werk "Ad locos planos et solidos isagoge" (Einführung in die ebenen und körperlichen Örter), das erstmals entscheidende Grundgedanken der analytischen Geometrie entwickelt. In den Jahren 1657 und 1658 lieferte Fermat eine Fülle anregender Sätze und Problemstellungen der Zahlentheorie, wobei er bei der Arithmetik von Diophantos von Alexandria anknüpfte.
Die wohl größte Berühmtheit erlangte Fermat durch den sogenannten
Großen Satz von Fermat, welcher aussagt, daß die Gleichung
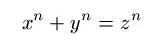
für keine ganze Zahl n größer 2 in den natürlichen Zahlen lösbar ist. 1905 stellte der Göttinger Professor Wolfskehl 100.000 Mark für denjenigen zur Verfügung, der diesen Satz beweisen konnte. Von da an liefen Tausende von sogenannten Beweisen ein, jedoch gelang der Beweis erst Andrew J. Wiles 1993.
Früher bewiesen werden konnte, nämlich erstmals durch Leibniz,
der Kleine Satz von Fermat, der lautet:
Wenn p eine Primzahl ist und a eine ganze Zahl, die sich nicht
ohne Rest durch p teilen läßt,
so hat die p-te Potenz von a bei Division durch p den Rest a.
Von Fermat stammt auch eines der nach Gauß schönsten Beispiele der Zahlentheorie, nämlich daß sich jede Primzahl der Form 4n + 1 eindeutig als Summe von zwei Quadraten darstellen läßt. Es besteht kein Zweifel, daß Fermat diesen Satz bewiesen hat, jedoch stammte die erste Veröffentlichung eines Beweises zu diesem Resultat aus dem Jahr 1749 von Euler.
Am 12. Jänner 1665 starb Pierre de Fermat in Castres bei Toulouse.